车吊点计算涉及多因素,一般根据物体重量、形状及吊运要求等,通过
车吊点位置的计算对于确保安全、高效地吊装作业至关重要,以下将详细介绍吊车吊点位置的计算公式及相关内容。
吊车吊点位置计算的基础原理
在计算吊车吊点时,需要考虑多个因素,包括被吊物体的重量、形状、重心位置以及吊车的起重能力等,其核心原理是保证吊车在吊装过程中受力平衡,避免出现倾翻等安全事故。

不同情况下吊点位置的计算公式
(一)规则形状物体(如块状物料、棒材等)
- 单吊点情况
- 当采用单吊点吊装形状规则、重心居中的物体时,吊点应位于物体的几何中心上方,对于一个长方体的块状物料,其重心在对角线的交点处,吊点就应设置在该交点正上方。
- 计算公式:如果物体的长、宽、高分别为(a)、(b)、(c),则重心坐标((x_c,y_c,z_c))为(\begin{cases}x_c=\frac{a}{2}\y_c=\frac{b}{2}\z_c=\frac{c}{2}\end{cases}),吊点位置即为((x_c,y_c,z_c + h)),h)为吊索与物体连接点到重心的垂直距离,一般根据吊索长度和吊装角度确定。
- 多吊点情况
- 对于较长的规则物体,如棒材,可能需要采用多吊点吊装,以两个吊点为例,假设棒材长度为(L),重量为(W),两个吊点距离棒材两端的距离分别为(l_1)和(l_2),且(l_1 + l_2 = L)。
- 根据力学平衡原理,有(\frac{l_1}{l_2}=\frac{F_2}{F_1}),F_1)和(F_2)分别为两个吊点所受的力,由于对称吊装时(F_1 = F_2),l_1 = l_2 = \frac{L}{2}),即两个吊点应分别位于棒材的四分之一处和四分之三处。
- 推广到(n)个吊点的情况,若物体长度为(L),各吊点间距应尽量相等,以保证受力均匀,相邻吊点之间的距离(d = \frac{L}{n 1})。
(二)不规则形状物体
- 估算重心法
- 对于不规则形状物体,首先需要估算其重心位置,一种常用的方法是分割法,将物体分割成若干个规则的小块,计算出每个小块的重心坐标和重量,然后根据力矩平衡原理计算整体重心坐标。
- 将物体分割成(n)个小块,第(i)个小块的重量为(Wi),重心坐标为((x{ci},y{ci},z{ci})),则整体重心坐标((x_c,y_c,z_c))的计算公式为: [ \begin{cases} xc=\frac{\sum{i = 1}^{n}Wix{ci}}{\sum_{i = 1}^{n}W_i}\ yc=\frac{\sum{i = 1}^{n}Wiy{ci}}{\sum_{i = 1}^{n}W_i}\ zc=\frac{\sum{i = 1}^{n}Wiz{ci}}{\sum_{i = 1}^{n}W_i} \end{cases} ]
- 确定重心后,吊点位置应设置在重心上方,并根据物体的形状和吊装要求进行适当调整,以确保吊装过程中的稳定性。
- 吊点反算法
- 在实际吊装中,有时需要根据吊车的起重能力和吊装条件来确定吊点位置,已知吊车的额定起重量(P),吊索与水平面的夹角为(\theta),物体重量为(W)。
- 根据受力分析,吊索的拉力(F = \frac{W}{n\sin\theta}),n)为吊索数量,为了保证吊车不超载,应满足(F\leq P)。
- 通过这个不等式可以反算出吊索与水平面的夹角(\theta),进而确定吊点的位置,当(n = 2)时,(\sin\theta=\frac{W}{2P}),根据三角函数关系可以计算出吊点的高度位置。
计算示例
假设有一个长方体形状的设备,长(a = 5m),宽(b = 3m),高(c = 2m),重量(W = 100kN),采用两个吊点吊装,吊索与垂直方向夹角为(30^{\circ})。
- 计算重心坐标 根据长方体重心计算公式,重心坐标为(\begin{cases}x_c=\frac{5}{2}=2.5m\y_c=\frac{3}{2}=1.5m\z_c=\frac{2}{2}=1m\end{cases})。
- 计算吊索拉力 因为有两个吊点,且吊索与垂直方向夹角为(30^{\circ}),所以吊索与水平面夹角为(60^{\circ})。 根据公式(F=\frac{W}{n\sin\theta}),可得(F=\frac{100}{2\times\sin60^{\circ}}\approx57.74kN)。
- 确定吊点位置 由于是两个吊点吊装长方体设备,为了保证受力均匀,两个吊点应在设备的重心两侧对称分布,假设吊点距离设备上表面的高度为(h),根据几何关系,(h = z_c + \frac{c}{2}\cot30^{\circ}=1 + 1\times\sqrt{3}\approx2.73m)。 在水平方向上,两个吊点距离重心的距离(l)可以根据设备的长度和宽度进行调整,一般取设备长度或宽度的一定比例,以保证吊装稳定性,取(l = \frac{a}{4}=1.25m),则两个吊点的平面位置坐标分别为((2.5 1.25,1.5))和((2.5 + 1.25,1.5)),即((1.25,1.5))和((3.75,1.5))。
实际应用中的注意事项
- 考虑吊车的性能参数
吊车的额定起重量、工作半径、起升高度等性能参数都会影响吊点位置的选择,在选择吊点时,必须确保吊车的各项工作参数满足吊装要求,避免超载和超出工作范围。
- 物体的悬挂状态
不同的悬挂状态会导致物体在吊装过程中的受力情况不同,采用兜吊时,吊索与物体的接触面积较大,需要考虑物体的强度和稳定性;采用锁吊时,吊点的位置和数量需要根据物体的形状和重量进行精确计算。
- 现场环境因素
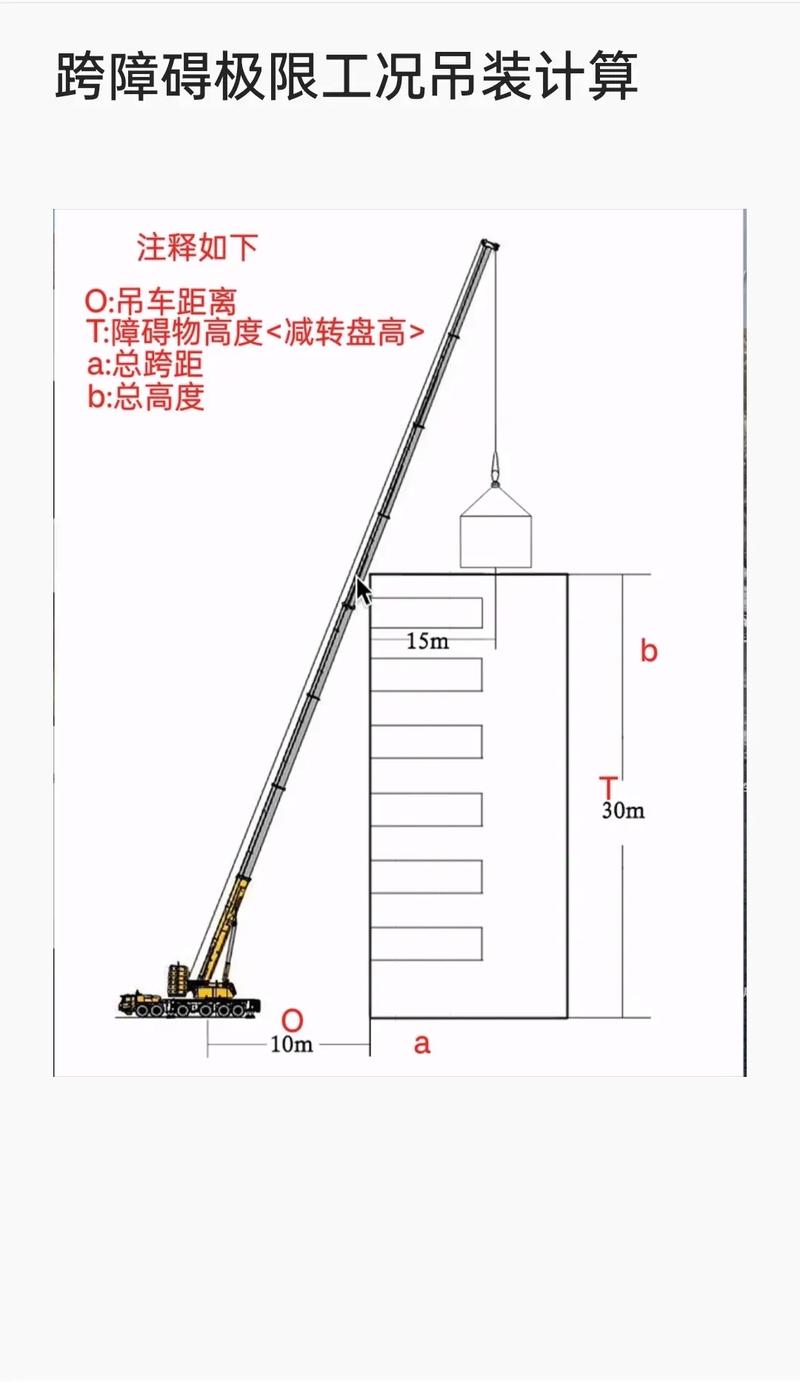
现场的空间限制、障碍物分布以及其他设备的位置等环境因素也会对吊点位置产生影响,在计算吊点位置时,需要充分考虑这些因素,确保吊装作业的安全进行。
 (图片来源网络,侵删)
(图片来源网络,侵删) - 安全系数的选取
为了确保吊装安全,在计算吊点位置和吊索拉力时,需要选取适当的安全系数,安全系数应根据吊车的类型、使用年限、吊装作业的重要性等因素综合考虑,一般取值在(1.2 2.0)之间。
以下是一个简单的表格,归纳了上述内容:
| 吊装情况 | 计算公式 | 说明 |
|---|---|---|
| 单吊点吊装规则物体 | 重心坐标((x_c,y_c,z_c)),吊点位置((x_c,y_c,z_c + h)) | 适用于形状规则、重心居中的物体 |
| 多吊点吊装规则物体(以两个吊点为例) | (\frac{l_1}{l_2}=\frac{F_2}{F_1}),对称吊装时(l_1 = l_2 = \frac{L}{2}) | 用于长条形规则物体,保证受力均匀 |
| 不规则形状物体估算重心 | (\begin{cases}xc=\frac{\sum{i = 1}^{n}Wix{ci}}{\sum_{i = 1}^{n}W_i}\yc=\frac{\sum{i = 1}^{n}Wiy{ci}}{\sum_{i = 1}^{n}W_i}\zc=\frac{\sum{i = 1}^{n}Wiz{ci}}{\sum_{i = 1}^{n}W_i}\end{cases}) | 将物体分割成小块计算整体重心 |
| 不规则形状物体吊点反算 | (\sin\theta=\frac{W}{nP}) | 根据吊车起重量和物体重量计算吊索角度,进而确定吊点位置 |
FAQs
问题1:吊车吊点计算时,安全系数如何确定? 答:安全系数的确定需要考虑多个因素,首先要根据吊车的类型,例如汽车吊、履带吊等,不同类型的吊车由于结构和使用工况的差异,其安全系数的取值范围可能有所不同,吊车的使用年限也很关键,新吊车相对性能较好,安全系数可适当取低值;而使用年限较长的吊车,考虑到部件磨损等因素,安全系数应取高值,吊装作业的重要性也会影响安全系数,对于一些关键设备、大型工程的重要构件吊装,安全系数要偏大,一般取值在1.2 2.0之间,以确保足够的安全保障。
问题2:在复杂现场环境中,如何考虑障碍物对吊点位置的影响? 答:在复杂现场环境中,首先要对障碍物的位置、大小和高度进行详细勘查,如果障碍物在吊装作业区域的下方,需要确保吊点位置的选择能使被吊物体在起升过程中避开障碍物,可能需要增大吊点与障碍物的水平距离或者提高吊点高度,若障碍物在周围,要考虑吊车回转半径和被吊物体的摆动范围,防止在吊装过程中被吊物体与障碍物发生碰撞。
标签: 吊点